η = V_air / V_subst.

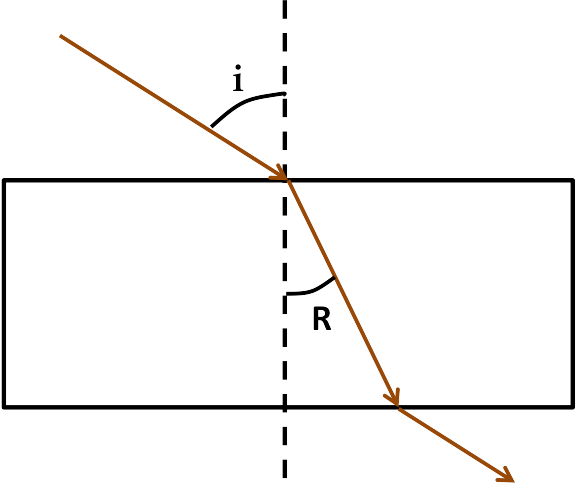
Angle of Refraction (R)

i = angle of incidence R = angle of refraction
Snell's Law: for calculation of Refractive Index (η) from angles of incidence and refraction

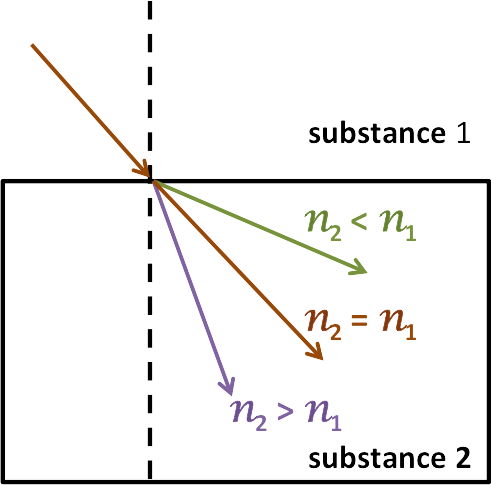
when substances are more dense, light travels at a low velocity & light ray bends toward the perpendicular when substances are less dense, light travels at a higher velocity than in denser materials & light ray bends away from the perpendicular

• Opaque - Light cannot pass through these materials regardless of how thin they are
  • This is commonly true of metals and minerals with metallic lusters

• Transparent - Light is able to pass through
  This class has two subclasses:
  • Isotropic - light travels through them with the same velocity in all directions because the atomic arrangement within the substance is either highly symmetrical or completely random.

    This class includes:

    • Isometric Minerals (highly symmetrical atomic arrangement)

    • Amorphous Materials - ex. glass, liquids &helip; (random atomic arrangement)

  • Anisotropic - the speed of light through these substances is direction-dependent because the atomic arrangement (and therefore, density of atoms) differs relative to the crystallographic axes within the substance.

    This class has two subclasses:

    • Uniaxial: have one "optic axis" or direction along which light does not split into two rays - all light travels at the same velocity. In all other directions through the crystal, light splits into 2 rays with mutually perpendicular vibration directions and different velocities.
      • Includes: Hexagonal (hex/hex & hex/rhomb), Tetragonal Crystals

    • Biaxial: have 2 optic axes or directions along which light does not split into two rays - all light travels at the same velocity. In all other directions through the crystal, light splits into 2 rays with mutually perpendicular vibration directions and different velocities.
      • Includes: Orthorhombic, Monoclinic & Triclinic Crystals

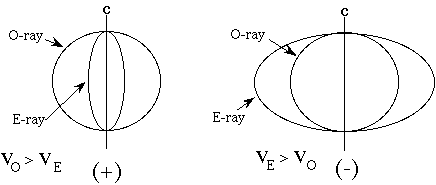
Uniaxial Ray Velocity Diagrams

Diameters reflect the VELOCITY that a light ray would have along a particular propagation direction (direction light ray travels relative to the crystal axes).

Diameters reflect the REFRACTIVE INDEX that a light ray would have along a particular propagation direction.

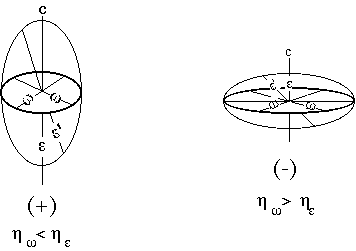
For any propagation direction (orientation of light ray passing through the crystal) the related refractive indicies are the diameters of the cross-section which is perpendicular to the propagation direction. In unixial crystals, one of these diameters will always be omega, the other will be epsilon or epsilon prime.

http://classes.colgate.edu/rapril/geol201/ Questions to: rapril@mail.colgate.edu Copyright 1997 © Colgate University.

Mineralogy Home page