

The First Day
When you enter the laboratory on the first day, you should bring the laboratory manual, your safety glasses and your duplicating notebook; you will not be allowed to work in the laboratory without both these items. It is also a good idea to bring a calculator.
Before you come to your first laboratory period, be sure you have read and understood the Chemical Safety section of the lab manual. You will be asked to sign the Laboratory Safety Agreement which is on the back cover of your lab manual. You should also have read the first laboratory exercise - How Big is an Atom? - and have a reasonable idea of what you will be doing in lab. Once in the laboratory, you will check in to a laboratory desk and locker, get oriented in the laboratory, become familiar with the safety equipment, and do the How Big is an Atom? experiment.
Note: Check all the glassware and crucibles in your lab desk, you may exchange any missing or broken glassware or crucibles without being charged during the first lab period only. After you sign your check-in sheets you are responsible for everything in your lab benches and will be charged for subsequent missing or broken items.
Experiment 1-006 Report Sheets: (pdf format)
This week you will determine the size of an atom by measuring the density of an elemental solid. You will choose Cu, Al or Ag and determine the size of a unit cell. Each of these metals has a unit cell that is cubic-closed packed or face-centered cubic..
A sample of the elemental solid and volumetric flasks are provided. The mass of several things must be accurately determined:
From these measurements the density of the sample can be calculated. Knowing the density and mass of the sample, the volume of the unit cell can be determined. From this information, the length of the unit cell edge and the radius of its component atoms can be calculated.
So how do we really do this ?
Well, to calibrate the actual volume of your volumetric flask (10.0 or 50.0 ), you take the difference of the masses of empty flask and the flask filled to the mark with distilled water (dH2O). Using the density of water (you need to measure the temperature of the water in the flask and look up the density that corresponds to that temperature on p.32 of the lab manual), you can calculate the volume of the flask: density = mass/volume so volume of flask = mass of dH2O/density.
To determine the density of your solid, you must find the mass of the metal in flask and the volume of the metal in the flask. The mass of the metal is simply the difference of the mass of the empty flask and the mass of the flask + metal. Finding the volume of the metal in the flask is a little less straightforward. You must first calculate the volume of the water over the metal. To do this you must first find the mass of the water over the metal (mass of flask/ metal/water - mass of empty flask) and then divide this mass by the density of water (at same temp as above). Now you'll have the volume of water above the metal, if you then subtract this volume from the volume of the flask (from above), you'll have the volume of the metal in the flask. Once you have the mass of the metal and the volume of the metal, you can easily find the density of the metal.
The next step is to find the mass of a unit cell of your metal. In order to do that you must calculate how many atoms are in a unit cell. Since all of the metals we used have a cubic-closed-packed (ccp) lattice:
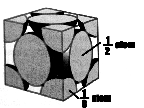
8 corner atoms x 1/8 of each per cell = 1 atom
6 face atoms x _ of each per cell = 3 atoms
Total atoms per unit cell = 4 atoms
Hence the mass of a unit cell (g) = mol. mass of metal (g/mole) x 4 atoms x 1mole/6.022 x 1023 atoms.
Volume of a unit cell = mass unit cell/density unit cell. The density of the unit cell is simply = density of the bulk metal (which you found above).
Once the volume of the unit cell has been determined, the rest
is geometry. For a cube with an edge length of l , the volume will be l3 ; conversely, the length
of the cell edge ( l ) is the cube
root of the cell volume ( ![]() ). Once the cell volume is known, the cell edge
length ( l ) can be calculated.
). Once the cell volume is known, the cell edge
length ( l ) can be calculated.
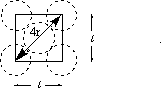
With a little help from Pythagoras the radius of the atom, r, can be determined from the length of the cell edge:
l2 + l2 = d2 and d = 4r then
2 l2 = d2 = (4r)2 = 16r2
Solving for r leads to: r = [(1/8)1/2 ]l